Partial Differential Equations with Boundary Conditions

Significant developments happened for Maple 2019 in its ability for the exact solving of PDE with Boundary / Initial conditions. The new functionality is described below, in 11 brief Sections, with 30 selected examples and a few comments. 

1. PDE and BC problems solved using linear change of variables 

PDE and BC problems often require that the boundary and initial conditions be given at certain evaluation points (usually in which one of the variables is equal to zero). Using linear changes of variables, however, it is possible to change the evaluation points of BC, obtaining the solution for the new variables, and then changing back to the original variables. This is now automatically done by the pdsolve command. 

 

Example 1: A heat PDE & BC problem in a semi-infinite domain: 

>

 

>

 

 

Note the evaluation points A and B. The method typically described in textbooks requires the evaluation points to be . The change of variables automatically used in this case is: 

>

 

 

so that pdsolve's task becomes solving this other problem, now with the appropriate evaluation points 

>

 

 

and then changing the variables back to the original {x, t, u} and giving the solution. The process all in one go: 

>

 

 

 

Example 2: A heat PDE with a source and a piecewise initial condition 

>

 

>

 

>

 

 

 

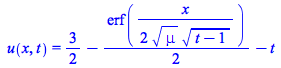Example 3: A wave PDE & BC problem in a semi-infinite domain: 

>

 

>

 

>

 

 

 

Example 4: A wave PDE & BC problem in a semi-infinite domain: 

>

 

>

 

>

 

 

 

Example 5: A wave PDE with a source: 

>

 

>

 

>

 

 

>

 

 

2. It is now possible to specify or exclude method(s) for solving 

Staring with Maple 2019, the pdsolve/BC solving methods can be indicated, either to be used for solving, as in to be tried in the order indicated, or to be excluded, as in . The methods and sub-methods available are organized in a table,  

 

>

 

 

So, for example, the methods for PDEs of first order and second order are, respectively, 

>

 

 

>

 

 

 

Some methods have sub-methods (their existence is visible in ): 

>

 

 

>

 

 

 

Example 6: 

>

 

>

 

>

 

 

>

 

 

Example 7: 

>

 

>

 

>

 

 

>

 

 

>

 

 

>

 

 

3. Series solutions for linear PDE and BC problems solved via product separation with eigenvalues that are the roots of algebraic expressions which cannot be inverted 

Linear problems for which the PDE can be separated by product, giving rise to Sturm-Liouville problems for the separation constants (eigenvalues) and separated functions (eigenfunctions), do not always result in solvable equations for the eigenvalues. Below are examples where the eigenvalues are respectively roots of a sum of Bessel functions and of a trigonometric equation .  

 

Example 8: This problem represents the temperature distribution in a thin circular plate whose lateral surfaces are insulated (Articolo example 6.9.2): 

>

 

>

 

>

 

 

In the above we see that the eigenvalue satisfies . When is the root of one single or function of integer order, the Maple functions and are used instead. That is the case, for instance, if we slightly modify this problem changing the first boundary condition to be instead of  

>

 

>

 

 

 

 

Example 9: This problem represents the temperature distribution in a thin rod whose left end is held at a fixed temperature of 5 and whose right end loses heat by convection into a medium whose temperature is 10. There is also an internal heat source term in the PDE (Articolo example 8.4.3): 

>

 

>

 

>

 

 

For information on how to verify or plot a solution like the one above, see the section "Sturm-Liouville problem with eigenvalues that are the roots of algebraic expressions which cannot be inverted" in the pdsolve with boundary conditions help page. 

 

4. Superposition method for linear PDE with more than one non-homogeneous BC 

Previously, for linear homogeneous PDE problems with non-periodic initial and boundary conditions, pdsolve was only consistently able to solve the problem as long as at most one of those conditions was non-homogeneous. The superposition method works by taking advantage of the linearity of the problem and the fact that the solution to such a problem in which two or more of the BC are non-homogeneous can be given as 

u = + ...,  where each is a solution of the PDE with all but one of the BC homogenized. 

 

Example 10: A Laplace PDE with one homogeneous and three non-homogeneous conditions: 

>

 

>

 

>

 

 

 

5. Polynomial solutions method: 

This new method gives pdsolve better performance when the PDE & BC problems admit polynomial solutions. 

 

Example 11: 

>

 

>

 

>

 

 

 

6. Solving more problems using the Laplace transform or the Fourier transform 

These methods now solve more problems and are no longer restricted to PDE of first or second order. 

 

Example 12: A third order PDE & BC problem: 

>

 

>

 

>

 

 

 

Example 13: A PDE & BC problem that is solved using Laplace transform: 

>

 

>

 

>

 

 

To see the computational flow, the solving methods used, and in which order they are tried, use 

>

 

 

Example 14:  

>

 

>

 

>

 

 

* trying method "SpecializeArbitraryFunctions" for 2nd order PDEs   -> trying "LinearInXT"   -> trying "HomogeneousBC" * trying method "SpecializeArbitraryConstants" for 2nd order PDEs * trying method "Wave" for 2nd order PDEs   -> trying "Cauchy"   -> trying "SemiInfiniteDomain"   -> trying "WithSourceTerm" * trying method "Heat" for 2nd order PDEs   -> trying "SemiInfiniteDomain"   -> trying "WithSourceTerm" * trying method "Series" for 2nd order PDEs   -> trying "TwoBC"   -> trying "ThreeBCsincos"   -> trying "FourBC"   -> trying "ThreeBC"   -> trying "ThreeBCPeriodic"   -> trying "WithSourceTerm"      * trying method "SpecializeArbitraryFunctions" for 2nd order PDEs         -> trying "LinearInXT"         -> trying "HomogeneousBC"            Trying travelling wave solutions as power series in tanh ...               Trying travelling wave solutions as power series in ln ...      * trying method "SpecializeArbitraryConstants" for 2nd order PDEs         Trying travelling wave solutions as power series in tanh ...            Trying travelling wave solutions as power series in ln ...      * trying method "Wave" for 2nd order PDEs         -> trying "Cauchy"         -> trying "SemiInfiniteDomain"         -> trying "WithSourceTerm"      * trying method "Heat" for 2nd order PDEs         -> trying "SemiInfiniteDomain"         -> trying "WithSourceTerm"      * trying method "Series" for 2nd order PDEs         -> trying "TwoBC"            Trying travelling wave solutions as power series in tanh ...               Trying travelling wave solutions as power series in ln ...         -> trying "ThreeBCsincos"         -> trying "FourBC"         -> trying "ThreeBC"         -> trying "ThreeBCPeriodic"         -> trying "WithSourceTerm"         -> trying "ThreeVariables"

 

* trying method "Laplace" for 2nd order PDEs         -> trying a Laplace transformation      * trying method "Fourier" for 2nd order PDEs         -> trying a fourier transformation

 

* trying method "Generic" for 2nd order PDEs         -> trying a solution in terms of arbitrary constants and functions to be adjusted to the given initial conditions      * trying method "PolynomialSolutions" for 2nd order PDEs      * trying method "LinearDifferentialOperator" for 2nd order PDEs      * trying method "Superposition" for 2nd order PDEs   -> trying "ThreeVariables" * trying method "Laplace" for 2nd order PDEs   -> trying a Laplace transformation * trying method "Fourier" for 2nd order PDEs   -> trying a fourier transformation

 

<- fourier transformation successful <- method "Fourier" for 2nd order PDEs successful

 

>

 

 

Reset the infolevel to avoid displaying the computational flow: 

>

 

7. Improvements to solving heat and wave PDE, with or without a source: 

Example 15: A heat PDE: 

>

 

>

 

>

 

 

To verify an infinite series solution such as this one you can first use pdetest  

>

 

 

To verify that the last condition, for is satisfied, we plot the first 1000 terms of the series solution with and make sure that it coincides with the plot of the right-hand side of the initial condition . Expected: the two plots superimposed on each other 

>

 

 

Example 16: A heat PDE in a semi-bounded domain: 

>

 

>

 

>

 

 

 

Example 17: A wave PDE in a semi-bounded domain: 

>

 

>

 

>

 

 

 

Example 18: A wave PDE with a source 

>

 

>

 

>

 

 

 

Example 19: Another wave PDE with a source 

>

 

>

 

>

 

 

8. Improvements in series methods for Laplace PDE problems 

Example 20: A Laplace PDE with BC representing the inside of a quarter circle of radius 1. The solution we seek is bounded as approaches 0: 

>

 

>

 

>

 

 

 

Example 21: A Laplace PDE for which we seek a solution that remains bounded as y approaches : 

>

 

>

 

>

 

 

 

9. Better simplification of answers: 

 

Example 22: For this wave PDE with a source term, pdsolve used to return a solution with uncomputed integrals: 

>

 

>

 

>

 

 

 

Example 23: A BC at is now handled by pdsolve: 

>

 

>

 

>

 

 

 

Example 24: A reduced Helmholtz PDE in a square of side Previously, pdsolve returned a series starting at , when the limit of the term is 0. 

>

 

>

 

>

 

 

 

10. Linear differential operator: more solutions are now successfully computed 

 

Example 25: 

>

 

>

 

>

 

 

 

Example 26: 

>

 

>

 

>

 

 

 

Example 27: 

>

 

>

 

>

 

 

 

 

11. More problems in 3 variables are now solved 

 

Example 28: A Schrödinger type PDE in two space dimensions, where ℏ is Planck's constant. 

>

 

>

 

>

 

 

 

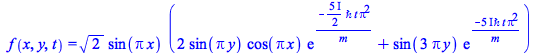Example 29: This problem represents the temperature distribution in a thin rectangular plate whose lateral surfaces are insulated yet is losing heat by convection along the boundary , into a surrounding medium at temperature 0 (Articolo example 6.6.3): 

>

 

>

 

>

 

 

 

Example 30: exercise 7.15 from Articolo's textbook, with six boundary/initial conditions: 

>

 

>

 

In this problem, there are three independent variables, therefore two eigenvalues (constants that appear separating variables by product) in the Sturm-Liouville problem. However, after solving the separated system and also for the eigenvalues, the second eigenvalue is equal to the first one, and it cannot be expressed in terms of known functions, because the equation it solves cannot be inverted. Its solution is, however, computable
 

>

 

 

 

For information on how to verify or plot a solution like the one above, see the section "Sturm-Liouville problem with eigenvalues that are the roots of algebraic expressions which cannot be inverted" in the pdsolve with boundary conditions help page. 

References 

Articolo, G. A. (2009). Partial differential equations and boundary value problems with Maple (2nd ed.). Amsterdam: Acad. Press/Elsevier.