Herausforderung
Jalal Soussi, ein Lehrer an einer Sekundarschule und Mitglied der Digital Transition Task Force in Belgien, suchte nach einer Lösung, um die Wissensvermittlung zu verbessern und es den Lehrern und Schülern zu erlauben, ihre Zeit und ihre Ressourcen optimal einzusetzen.
Lösung
Soussi untersuchte die Fähigkeiten von Maple, die Schüler zu motivieren und den Lernprozess zu vereinfachen. Er entwickelte eine Math App, um die Fähigkeiten von Maple anhand der Lösung verschiedener Probleme zu demonstrieren.
Ergebnis
Soussi fand heraus dass Maple ist eine ideale Umgebung ist, um individualisierte Lernpfade für Schüler zu erstellen, denn es ist benutzerfreundlich und die Schüler können darin experimentieren, um ihr Verständnis wichtiger Konzepte zu vertiefen.
Moderne digitale Lernwerkzeuge verändern die Art und Weise, in der Ausbildung vermittelt wird. Sie bieten neue Möglichkeiten, die Ausbildung für die Schüler effizienter zu machen, ihnen mehr mit auf den Weg zu geben, und es lässt die Dozenten ihre Zeit und Ressourcen besser einsetzen. Jalal Soussi, ein Lehrer an einer Sekundarschule in Belgien, hat die Fähigkeiten von Maple zur Optimierung der Ausbildung untersucht und seiner Erkenntnisse unlängst vorgestellt.
Neben seiner Rolle als Lehrer arbeitet Soussi auch als Trainer im Bereich des computergestützten Sprachenlernens (CALL) und ist Mitglied der Digital Transition Task Force im Rahmen einer belgischen Exzellenzinitiative für die Ausbildung. Soussi hat viel und lange mit Maple gearbeitet und in jüngster Zeit den Einsatz der Software für „Optimization Teaching“ auf der Grundlage einer Reihe von ihm entwickelter Mathematik-Apps untersucht. Er hat dabei die Möglichkeiten betrachtet, die Schüler mit Hilfe von Maple zu motivieren und das Lernen zu vereinfachen, um es so auf eine neue Weise zu optimieren. Laut Soussi bietet die Technologie von Maplesoft hierfür verschiedene hilfreiche Features:
Soussi hat Maple gewählt, weil es ein umfassend ausgestattetes mathematisches Softwarewerkzeug mit Fähigkeiten zur formalen Berechnung ist und präzise Lösungen zu vielen Problemen liefert. „Außerdem ist Maple ein mächtiges Werkzeug für numerische Berechnungen mit fortschrittlichen Features, einschließlich interaktiver 2D- und 3D-Schnittstellen für die grafische Visualisierung, Audio und Video“, sagte er. „Mit seinen Paketen, Math Apps und Tutorials kann man viele mathematische Konzepte ansprechen, darlegen, Annahmen dazu machen, sie vorführen und verstehen.“
Soussi ist der Ansicht, dass Maple alles mit sich bringt, was zum Experimentieren mit der Mathematik benötigt wird, d.h. das jeweilige Thema in einer originellen und ansprechenden Weise anzugehen, die den Entdeckergeist und die die Intuition herausfordert. „Maple ist einfach zu erlernen und dank der Online-Hilfe, z.B. den ständig verfügbaren Tutorials, braucht man das Handbuch fast nie in die Hand zu nehmen“, sagte er.
Das folgende Beispiel zeigt anhand einer von Soussi entwickelten Math App die Fähigkeiten von Maple.
Problem
Um eine Trainingssequenz zur Optimierung in Maple zu untersuchen, wählte Soussi 20 verschiedene Probleme nach dem folgenden Muster: „Bestimmen Sie die Abmessungen eines geraden Kreiszylinders mit dem größten Volumen, der sich in einer Kugel mit dem Radius 4 unterbringen lässt.“
Soussi wählte die vorgeschlagene Struktur wegen ihrer Flexibilität, die es ihm erlaubte, die verschiedenen Maple-Umgebungen zu untersuchen. Bei der Vorbereitung arbeitete er an geometrischen Grundeigenschaften des Zylinders (Abbildung 1) auf der Grundlage von Sprachanweisungen, um verschiedene Formeln herzuleiten (Volumen, Oberfläche usw.).
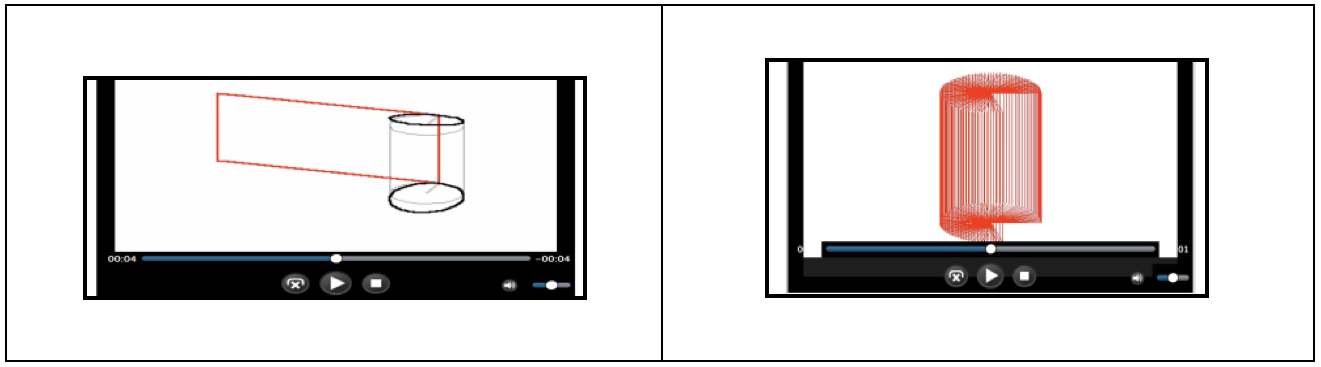
Abbildung 1
Er arbeitete interaktiv mit dem Konzept eines Rotationskörpers, der durch die Rotation einer konstanten Funktion um die Achse entsteht. Daran konnte er das Konzept der Integralrechnung aufzeigen, ohne es weiter vertiefen zu müssen (Abbildung 2).
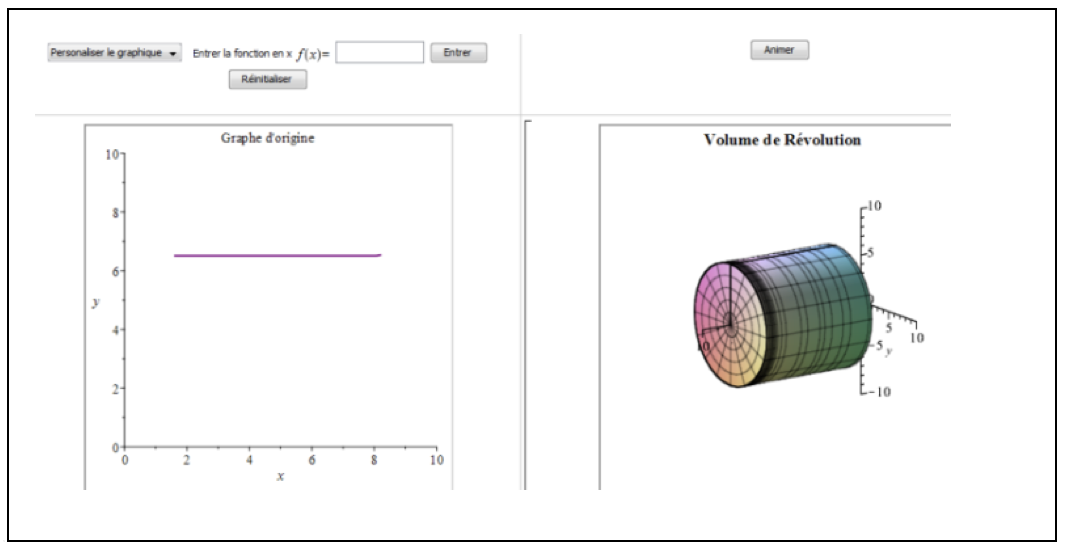
Abbildung 2
Soussi verweist die Anwender anschließend auf eine andere App, die beide Abbildungen des Problems zusammenführt. Durch die interaktive Annäherung an das Volumen einer Kugel mit Zylindern können die Anwender einfach und effizient Konzepte wie Grenzwerte und Reihenkonvergenz erlernen.
Problemlösung
Um das Problem zu lösen, können die Anwender verschiedene Ansätze wählen. Die folgenden Techniken schlägt Soussi in seiner Forschung vor:
Dynamische Animation
Die Anwender können mehrere bewegliche 3D-Objekte erzeugen, die durch die verschiedenen Variablen des Problems gesteuert werden (Höhe und Radius des Zylinders im Fall des Beispielproblems) (Abbildung 3). Damit lässt sich die räumliche Wahrnehmung dieser Darstellungen verbessern.
Abbildung 3
Lösen durch Ausprobieren
Soussi zeigt die Möglichkeit, den Variablen eine Wertetabelle zuzuordnen (Abbildung 4). Lernende können sich durch interaktives Steuern der Variablen des Problems digital an die optimale Lösung annähern.
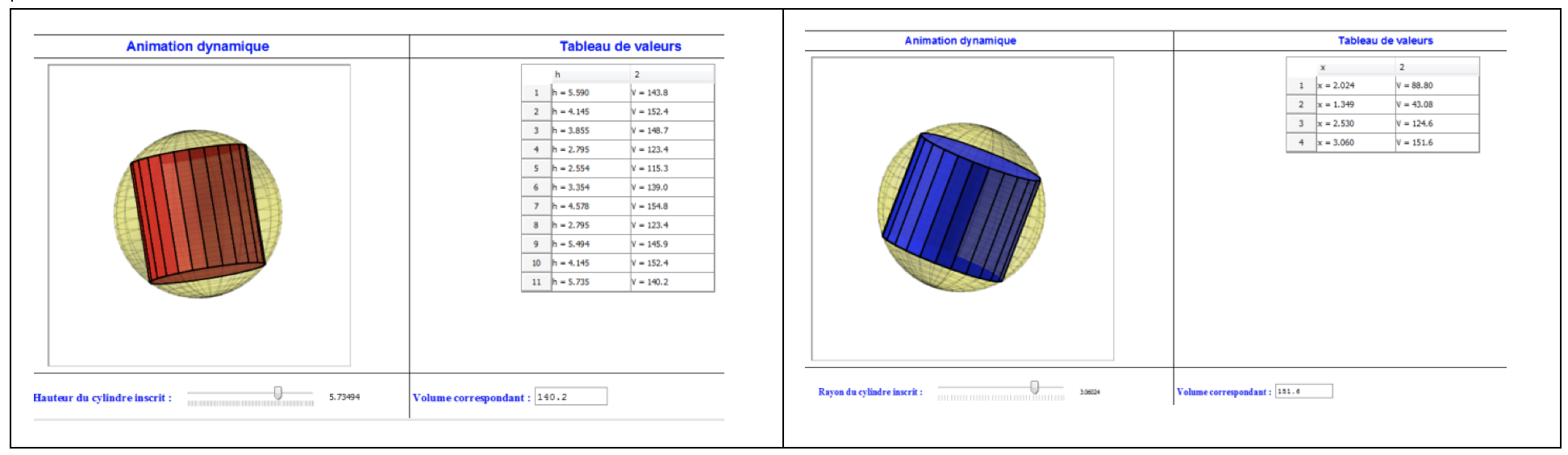
Abbildung 4
Analytische Lösung
Soussi führte aus, dass eine gründliche Analyse der Optimierungsfunktion(en) – Definitionsbereich, Ableitungen, Monotonie, besondere Punkte, Graph – unabhängig von der Form der Funktion durchgeführt wird, und dies entweder durch den Aufruf der entsprechenden Maple-Befehle, wenn der Lernende diese bereits kennt, oder intuitiv mit Clickable Math, einem einzigartigen Konzept in Maple, das dem Anwender, der die Software noch nicht so gut kennt, diesen Vorgang leichter macht. Mit dem ‚Tutorials‘-Werkzeug kann man die verschiedenen Ergebnisse eigenständig überprüfen (Abbildungen 5-A und 5-B).
Abbildung 5-A
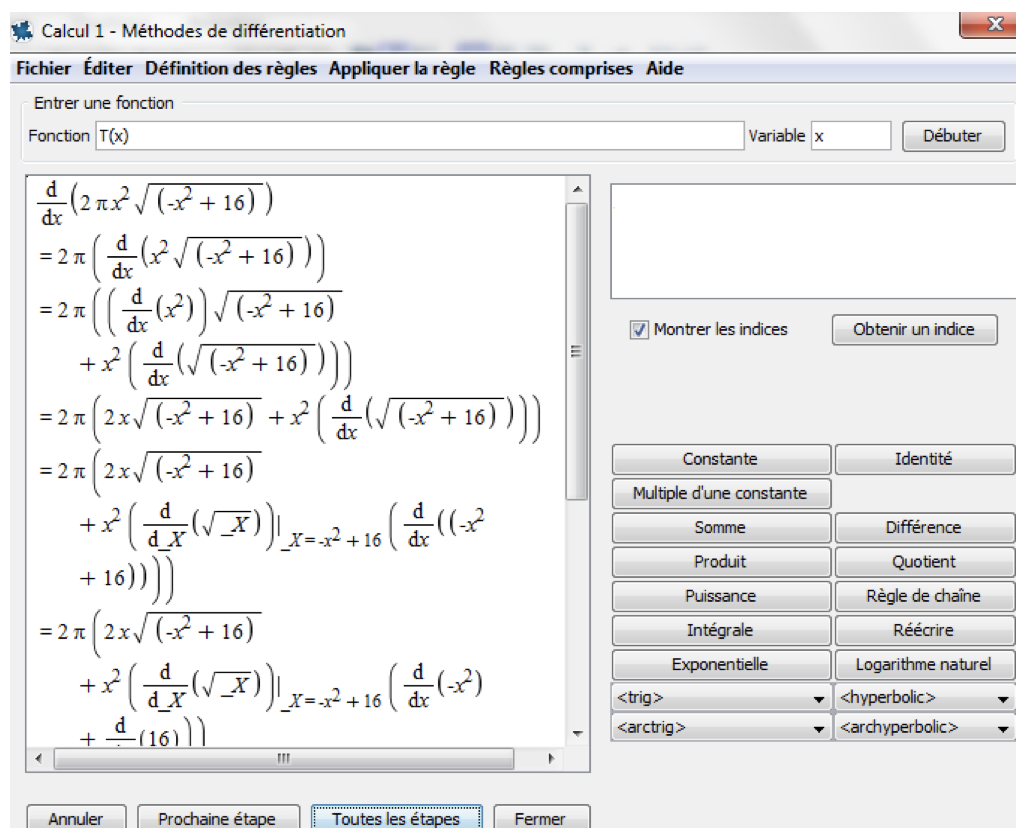
Abbildung 5-B
Als Beispiel führt Soussi die folgende Optimierungsfunktion an, die dann entsteht, wenn über den Radius des Zylinders vorgegangen wird:
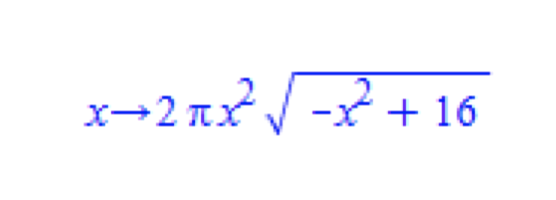
Er zeigt die folgenden Beispiele alternativer Lösungswege auf:
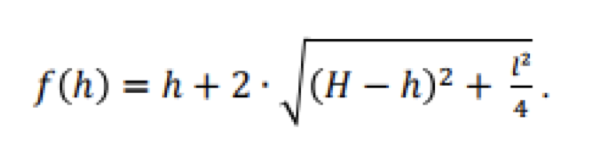
„Hierfür sind mehrere Ansätze möglich, die alle in Maple leicht untersucht werden können“, erklärte hierzu Soussi. Ein gutes Beispiel für diesen Ansatz ist, die Funktion zu quadrieren und dann grafisch oder analytisch zu überprüfen, ob das Maximum an der gleichen Stelle auftritt wie bei der Ausgangsfunktion (Abbildungen 6-A und 6-B).
Abbildung 6-A
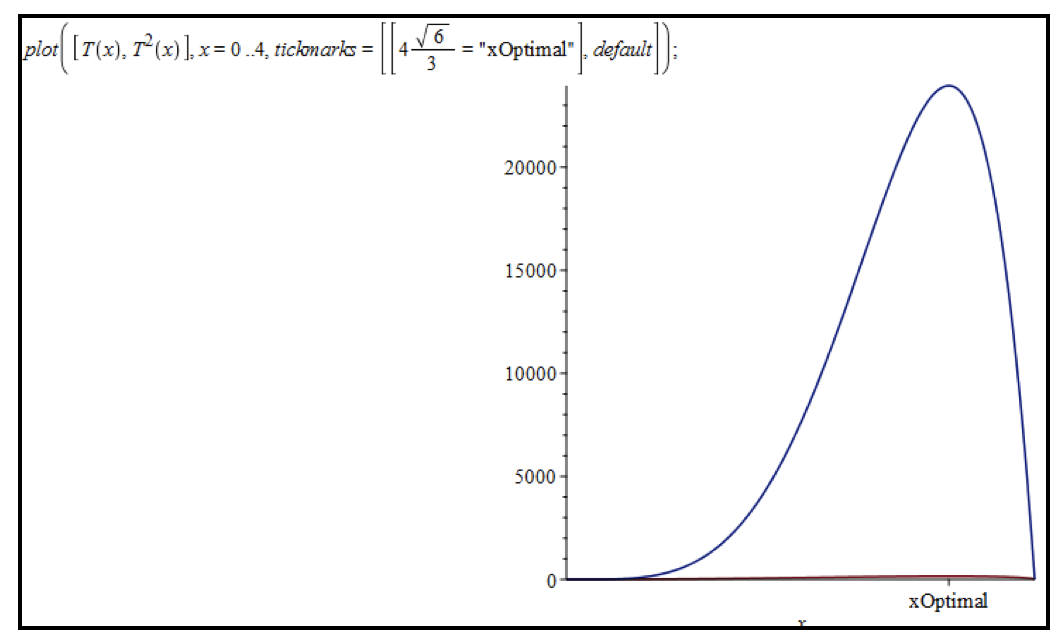
Abbildung 6-B
Visuelle Synthese
„Der Graph einer Funktion wird oft als statisches Objekt angesehen und seine Verbindung zu einem Phänomen ist für den Lernenden offenbar nicht einfach herzustellen“, sagte Soussi. „Die große Anzahl von interaktiven Komponenten in Maple erlaubt es den Anwendern, interaktiv viele Variablen des Problems zu verändern, um verschiedene Konzepte zu veranschaulichen: die Tangente (an der ursprünglichen Funktion), das Vorzeichen (der ersten Ableitung) und die Kurvenkrümmung (mit der zweiten Ableitung).“ Dies ist in der folgenden Abbildung 7 gezeigt.
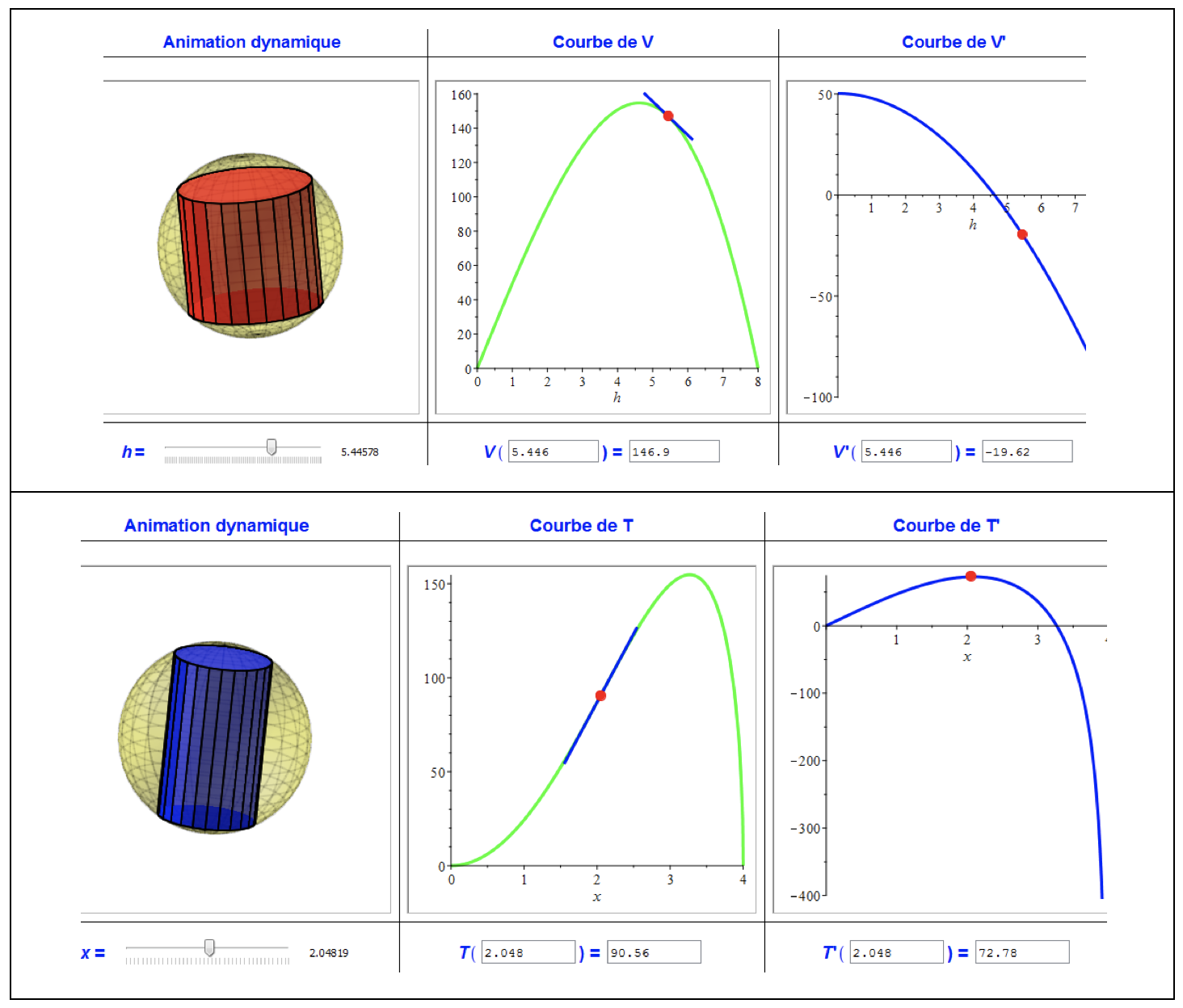
Abbildung 7
Das von Soussi erstellte Video “Optimierung mit Maple” zeigt, wie er Maple einsetzt.
Schlussfolgerung
„Damit die Lernenden dieses Thema wirklich verstehen, ist es notwendig, dass sie eigenständig daran arbeiten“, sagte Soussi.
Soussi hat mit anderen Softwarelösungen experimentiert, um das Problem in derselben Weise anzugehen. Seiner Meinung nach ist Maple die ideale Lösung. „Tatsächlich unterbrechen die meisten Lehrbücher und anderen Lernmittel in einer ähnlichen Situation die Erkundung des Themas“, schloss er. „Mit Maple können die Lernenden diese Konzepte hingegen tiefer erkunden und dadurch optimal lernen.“
Kontaktieren Sie Maplesoft, um zu erfahren, wie Maple bei Ihren Projekten angewandt werden kann.
